Currently Empty: ₹0.00

DAA Important Questions with Answer Diagram and Example(Unit-wise)
Unit 1: Sorting and Analysis
1. Sorting
- Merge Sort
- Solution: Merge Sort follows the divide and conquer approach. It divides the array into two halves, sorts them recursively, and then merges them in sorted order.
- Steps:
- Divide the unsorted array into two halves.
- Recursively sort the two halves.
- Merge the sorted halves.
- Example–
Input: [38, 27, 43, 3, 9, 82, 10]
Output: [3, 9, 10, 27, 38, 43, 82]
- Quick Sort
- Solution: Quick Sort selects a pivot, partitions the array such that elements smaller than the pivot go to the left and larger ones go to the right, and recursively sorts the subarrays.
- Steps:
- Choose a pivot element.
- Partition the array around the pivot.
- Recursively apply Quick Sort to the subarrays.
- Example:
Input: [10, 80, 30, 90, 40, 50, 70]
Output: [10, 30, 40, 50, 70, 80, 90]

- Heap Sort
- Solution: Heap Sort uses a binary heap structure to repeatedly extract the maximum element and place it at the end.
- Steps:
- Build a max heap from the array.
- Swap the first and last elements.
- Reduce heap size and repeat the heapify process.
- Example:
Input: [4, 10, 3, 5, 1]
Output: [1, 3, 4, 5, 10]

2. Recurrence Relation
- Using Master Theorem:
- Standard form: T(n) = aT(n/b) + f(n)
- Compare f(n) with n^(log_b(a)) to determine time complexity.
- Using Recursion Tree:
- Break down the recursive calls to find the overall cost.

3. Growth of Functions
- Big O (O) – Upper Bound
- Represents the worst-case scenario.
- It provides an upper limit on the growth rate of a function.
- It tells us that an algorithm will not take more than a certain amount of time or space.
- Example: If an algorithm has a time complexity of O(n²), it means the running time will not exceed a quadratic function of the input size.

- Big Theta (Θ) – Tight Bound
- Represents the average-case scenario.
- It gives both upper and lower limits, meaning the function grows at a specific rate within constant factors.
- It describes the exact asymptotic behavior.
- Example: If an algorithm has a time complexity of Θ(n²), it means the running time grows precisely at a quadratic rate, no more, no less.
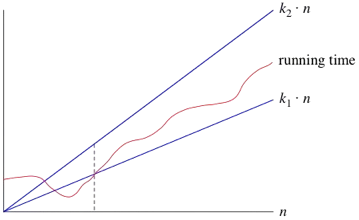
- Big Omega (Ω) – Lower Bound
- Represents the best-case scenario.
- It provides a lower limit on the growth rate of a function.
- It tells us that an algorithm will take at least a certain amount of time or space.
- Example: If an algorithm has a time complexity of Ω(n²), it means the running time will take at least a quadratic function of the input size.

Unit 2: Advanced Data Structures
1. Red-Black Tree
- A self-balancing binary search tree ensuring O(log n) operations.
- Properties:
- Every node is either red or black.
- The root is always black.
- No two consecutive red nodes.
- Every path has the same number of black nodes.
- Example: Insertion and rebalancing steps.

2. Binomial Heap
A binomial heap is a collection of binomial trees that satisfy the heap property.

Structure of Binomial Heap:
- A binomial heap consists of binomial trees, which are recursively defined.
- A binomial tree of order kk has:
- A root node with kk child binomial trees of orders 0,1,2,…,k−10, 1, 2, \dots, k-1.
- The number of nodes in a binomial tree of order kk is 2k2^k.
- The trees are ordered by their sizes, meaning a binomial heap of nn nodes will have trees whose orders correspond to the binary representation of nn.
Operations on Binomial Heap:
- Insert (O(log n))
- A new key is inserted as a single-node binomial tree (order 0).
- The new tree is merged into the existing heap using the merge operation.
- The process involves combining trees of the same order to maintain the binomial heap structure.
- Merge (Union) (O(log n))
- Combines two binomial heaps into one by merging their binomial trees.
- Trees of the same order are combined recursively, ensuring that no two trees of the same order exist in the final heap.
- The merge process follows a logic similar to binary addition.
- Extract Min (O(log n))
- Finds and removes the smallest key (minimum element) from the heap.
- The tree containing the minimum element is removed, and its subtrees are separated into a new heap.
- The new heap is merged back with the remaining heap to restore the binomial heap structure.
Advantages of Binomial Heap:
- Efficient merging of heaps, making it useful in applications requiring frequent merges.
- Supports logarithmic time complexity for key operations like insertion and extraction.
- Well-suited for applications like priority queues and graph algorithms (e.g., Dijkstra’s algorithm).
3. B-Tree
- A balanced multiway search tree used in databases. B-Trees are widely used because they efficiently manage large data while ensuring fast access and updates.

Operations on B-Trees:
- Search (O(log n))
- Similar to binary search, the algorithm compares the key with node values and navigates to the correct subtree.
- Due to the balanced structure, search operations take logarithmic time.
- Insertion (O(log n))
- A new key is inserted into the appropriate node while maintaining sorted order.
- If a node exceeds the maximum allowed keys, it is split, and the middle key is moved up to the parent.
- Splitting may propagate to the root, increasing the tree height.
- Deletion (O(log n))
- A key is removed while ensuring balance.
- If deletion causes a node to have fewer keys than the minimum required, keys are borrowed or nodes are merged.
- Similar to insertion, merging can propagate upwards, affecting tree height.
Advantages of B-Trees:
- Fast access: Logarithmic time complexity for search, insert, and delete operations.
- Minimized disk I/O: Optimized for large-scale storage applications.
- Balanced structure: Ensures efficient query performance even with large datasets.
- Scalability: Handles massive amounts of data efficiently.
Applications of B-Trees:
- Database indexing (e.g., MySQL, PostgreSQL).
- File systems (e.g., NTFS, ext4).
- Storage systems requiring efficient read/write operations.
4. Fibonacci Heap (Less Important)
- A heap supporting fast decrease-key operations.
- Operations: Insert, Union, Extract Min.

Operations:
- Insert (O(1) amortized): Adds a new element to the root list without restructuring.
- Union (O(1) amortized): Merges two heaps by combining their root lists.
- Extract Min (O(log n) amortized): Removes the smallest element and consolidates trees.
- Decrease-Key (O(1) amortized): Reduces a node’s key and moves it to the root list if needed.
- Delete (O(log n) amortized): Decreases a key to negative infinity and extracts the minimum.
Advantages:
- Fast decrease-key operation, useful in graph algorithms.
- Efficient for frequent priority updates.
Disadvantages:
- Complex implementation and higher constant factors.
Applications:
Dijkstra’s algorithm, network optimization, and priority scheduling.
Unit 3: Optimization Problems
1. Convex Hull and Searching

- Convex Hull algorithms like Graham’s scan for finding the outer boundary. The Graham’s Scan algorithm finds it in O(nlogn)O(n \log n) time by:
- Find the pivot: Select the point with the lowest y-coordinate (or lowest x if y’s are tied).
- Sort points by polar angle relative to the pivot.
- Construct the hull: Use a stack to process the points, keeping only those that form a counter-clockwise turn with the last two points.
- Time Complexity: O(nlogn)O(n \log n).
-
Example:
For points (0,0),(2,1),(1,3),(3,2),(4,0)(0, 0), (2, 1), (1, 3), (3, 2), (4, 0), the convex hull is:
(0,0),(4,0),(3,2),(1,3)(0, 0), (4, 0), (3, 2), (1, 3)
Applications:
- Computer graphics, collision detection, robotics, GIS.
2. Knapsack Problem

- Problem: Given a set of items with weights and profits, find the maximum profit without exceeding a weight limit.
- Dynamic Programming Solution:
- Use a 2D table where each entry represents the maximum profit for a given weight and item set.
- For each item, decide whether to include it or exclude it based on the maximum profit achievable.
- Time Complexity: O(nW)O(nW), where nn is the number of items and WW is the weight capacity.
3. Prim’s and Kruskal’s Algorithm

- Prim’s Algorithm:
- Start from an arbitrary node, adding the minimum weight edge to grow the MST.
- Use a priority queue to select the next closest vertex.
- Time Complexity: O(ElogV)O(E \log V), where EE is edges and VV is vertices.

- Kruskal’s Algorithm:
- Sort all edges in ascending weight order.
- Use a union-find structure to add edges to the MST, ensuring no cycles are formed.
- Time Complexity: O(ElogE)O(E \log E), dominated by sorting edges.
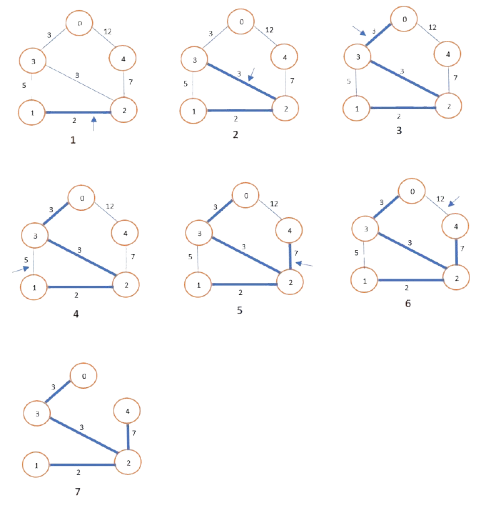
4. Dijkstra’s Algorithm
- Problem: Find the shortest path in a graph with non-negative edge weights.

- Greedy Approach:
- Use a priority queue to always pick the node with the smallest tentative distance.
- Update distances to neighbors and repeat until all nodes are processed.
- Time Complexity: O((V+E)logV)O((V + E) \log V), where VV is vertices and EE is edges.
5. Bellman-Ford Algorithm (Less Important)

- Problem: Find the shortest path in graphs with negative weights, and detect negative weight cycles.
- Dynamic Programming Approach:
- Relax all edges repeatedly up to V−1V-1 times (where VV is the number of vertices).
- Check for negative cycles by seeing if further relaxation is possible.
- Time Complexity: O(VE)O(VE), where VV is vertices and EE is edges.
Unit 4: Advanced Algorithms
1. Knapsack (Dynamic Programming)

- Problem: Maximize profit without exceeding a weight limit.
- Dynamic Programming Solution:
- Define a 2D DP table
dp[i][w], whereiis the number of items andwis the weight. - For each item, choose between including or excluding it based on whether it increases the profit without exceeding the weight.
- Fill the table iteratively based on previous results.
- Time Complexity: O(nW)O(nW), where nn is the number of items and WW is the weight capacity.
- Define a 2D DP table
2. Warshall’s and Floyd’s Algorithm
- Warshall’s Algorithm: Computes transitive closure of a directed graph, determining if there is a path between every pair of vertices.
- Time Complexity: O(V3)O(V^3), where VV is the number of vertices.
- Floyd-Warshall Algorithm: Computes the all-pairs shortest paths for a graph with both positive and negative weights.
- Iteratively update the shortest paths between every pair of vertices using an intermediate vertex.
- If a shorter path is found via an intermediate vertex, update the path.
- Time Complexity: O(V3)O(V^3), where VV is the number of vertices.
3. Backtracking
![]()
- Method: Explore all possible solutions recursively and backtrack when a solution path is invalid or incomplete.
- Start with an empty solution and attempt to extend it by adding one element at a time.
- If the current solution doesn’t lead to a valid complete solution, backtrack and try another option.
- Applications: Solving combinatorial problems like Sudoku, N-Queen, or the Hamiltonian path.
- Time Complexity: Depends on the problem; often exponential in nature.
4. Travelling Salesman Problem (TSP)
- Problem: Find the shortest possible route that visits every city once and returns to the origin.
- Dynamic Programming Solution (Held-Karp Algorithm):
- Use a DP table to store the shortest path covering each subset of cities and the last city in the subset.
- Solve recursively by considering each possible next city and updating the minimum cost.
- Time Complexity: O(n22n)O(n^2 2^n), where nn is the number of cities.

- Approximation:
- Greedy Heuristic: Start from an arbitrary city, always travel to the nearest unvisited city.
- Christofides’ Algorithm: Provides a 3/2 approximation for metric TSP (triangle inequality holds).
- Time Complexity for Approximation: O(n2)O(n^2).
5. N-Queen Problem
- Problem: Place N queens on an N×N chessboard such that no two queens threaten each other (no same row, column, or diagonal).
- Backtracking Solution:
- Place queens row by row, checking for conflicts in columns and diagonals.
- Backtrack when a placement leads to a conflict.
- Continue until all queens are placed safely.
- Time Complexity: Typically O(N!)O(N!) due to the factorial number of possible placements.






